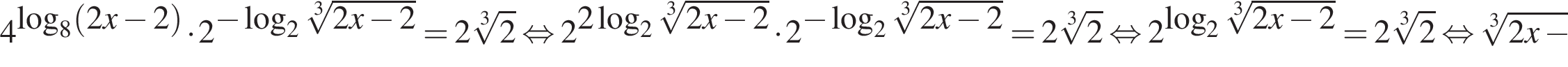1. Тип 1 № 3855 

Источник: Реальная версия ЕНТ по математике 2021 года, вариант 3. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
Классификатор алгебры: 1\.3\. Преобразования алгебраических дробей, 1\.4\. Вычисление степей и корней
Числовые алгебраические выражения. Задания для подготовки
i
Вычислите Broken TeX
1) 25
2) 245
3) 49
4) 135
Решение. Вычислим:
Broken TeX
Правильный ответ указан под номером 3.
Ответ: 3
3855
3
Источник: Реальная версия ЕНТ по математике 2021 года, вариант 3. Отредактировано редакцией Решу ЕНТ в формат актуальной демоверсии
Классификатор алгебры: 1\.3\. Преобразования алгебраических дробей, 1\.4\. Вычисление степей и корней