Тип Д20 A20 № 1555 
Задания реальной версии ЕНТ 2021 года на позиции 20
i
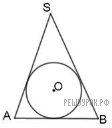 Из конуса вырезали шар наибольшего объёма. Найдите отношение объёма срезанной части конуса к объёму шара, если осевое сечение конуса — равносторонний треугольник.
Из конуса вырезали шар наибольшего объёма. Найдите отношение объёма срезанной части конуса к объёму шара, если осевое сечение конуса — равносторонний треугольник.
1) Broken TeX
2) Broken TeX
3) Broken TeX
4) Broken TeX
5) Broken TeX
Решение. Речь, разумеется, идет о шаре, вписанном в конус. Пусть образующая конуса равна 6x. Рассмотрим осевое сечение конуса. В нем от конуса останется равносторонний треугольник со стороной 6x, а от шара — вписанная в этот треугольник окружность. Ее радиус равен трети высоты, она же медиана и биссектриса, этого треугольника, то есть
Broken TeX
Объем шара равен
Broken TeX
Радиус основания конуса равен 3x, высота равна высоте осевого сечения, то есть Broken TeX Значит, объем конуса равен
Broken TeX
Тогда объем оставшейся части конуса равен
Broken TeX
Поэтому отношение равно
Broken TeX
Правильный ответ указан под номером 4.
Ответ: 4
Из конуса вырезали шар наибольшего объёма. Найдите отношение объёма срезанной части конуса к объёму шара, если осевое сечение конуса — равносторонний треугольник.
